Is Subsequence problem results
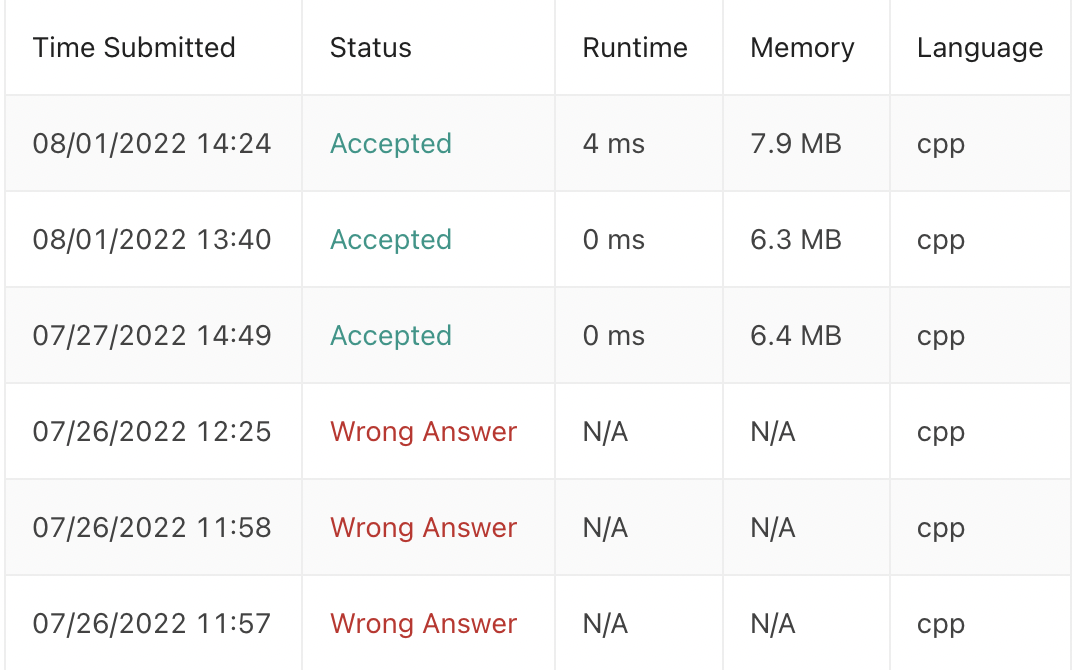
First Blood
Easiest method. Two-pointer. Traversing each string, update the index of “s” when finding the same character in t, else only update the index of “t”.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
{
bool isSubsequence(string s, string t) {
int j = 0;
for(int i = 0; i < t.length() && j < s.length(); i++)
{
if(t[i] == s[j])
j++;
}
if(j == s.length())
{
return true;
}
else
{
return false;
}
}
}
Double Kill
Using a recursive method. The idea behind this method is similar to the first method. By recursively checking if the last characters of the strings are matching.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
{
bool isSubs(string& s, string& t, int m, int n)
{
if(m == 0)
return true;
if(n == 0)
return false;
// If last characters of two
// strings are matching
if (s[m - 1] == t[n - 1])
return isSubs(s, t, m - 1, n - 1);
// If last characters are
// not matching
return isSubs(s, t, m, n - 1);
}
bool isSubsequence(string s, string t) {
return isSubs(s,t,s.length(),t.length());
}
}
Triple Kill
Using the longest common subsequence method and dynamic programming. This method is not straightforward as the first two methods, but it offers another way to solve this problem, and also learn the knowledge of the lcs and the dp.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
{
int longestCommonSubsequence(string& s, string& t) {
int m = s.length(), n = t.length();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
dp[i][j] = (s[i-1] == t[j-1]) ? dp[i-1][j-1] + 1 : max(dp[i][j-1], dp[i-1][j]);
}
}
return dp[m][n];
}
bool isSubsequence(string s, string t) {
return s.length() == longestCommonSubsequence(s,t);
}
}
