After setting up the environment for Smplify, run the code as followed:
1
2
conda activate smpl
python fit_3d.py ../ --out_dir ../smpl_lsp --viz
This script fits the SMPL model to LSP data, the results were stored in ../smpl_lsp.
Let’s go deeper into the source code along with the paper.
Data Preparation
Load LSP images and predicted 2D joints by DeepCut CNN stored in “est_joints.npz” including joint 2D position in image coordinate and confidence.
Fit SMPL model to a single image
step 1: Init the models
As said in the paper, this project use one of three shape models of SMPL: male, female, and gender-neutral. If gender is known, use the appropriate model. In the script, the gender for each data set was determined by the “lsp_gender.csv” file. Once the gender was determined, the SMPL model and the sph_regs(the regressor model for body shape approximation with capsules) used for interpenetration prevention were determined too.
1
2
3
4
5
6
7
8
9
10
if not use_neutral:
gender = 'male' if int(genders[ind]) == 0 else 'female'
if gender == 'female':
model = model_female
if use_interpenetration:
sph_regs = sph_regs_female
elif gender == 'male
model = model_male
if use_interpenetration:
sph_regs = sph_regs_male
step 2: Create pose prior term
The use of pose prior term is to favor probable poses over improbable ones. By fitting a Mixture Gaussians Model(8 gaussians) to 1 million poses(The GMM over CMU motion capture data), then scoring the new data point(the estimated pose), the GMM can tell the poses that are significantly different from the rest of the data. In English, the more common pose will have a higher score(the probability distribution function value). In the equation, its negative logarithm will be closer to 0. 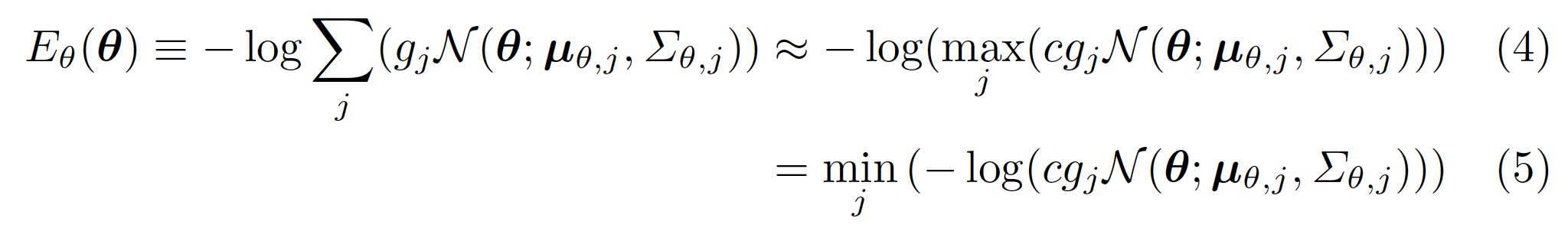 The GMM model was stored in smpl_public/code/models/gmm_08.pkl The mean pose was used to be the initial pose for the optimization process.
The GMM model was stored in smpl_public/code/models/gmm_08.pkl The mean pose was used to be the initial pose for the optimization process.
step 3: Estimate the camera translation and body orientation
The camera translation and body orientation were optimized based on torso joints including hips and shoulders. The camera rotation was set as an identity, in my opinion, this is because the rotation of the camera and the body orientation might be biased. The focal length of the camera was fixed to 5000, and not optimized because the problem will be too unconstrained to optimize it together with camera translation. Specifically, the depth of camera translation was first initialized via a similar triangle of torso joints. Then project the SMPL joints to the image using the camera with initialized depth, rotation and given focal length. An optimization function is here to optimize camera translation and body orientation which minimizes the distance between predicted 2D joints and estimated 2D joints on torso joints. A regularizer for the camera translation is to constrain the change of the camera translation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# optimize for camera translation and body orientation
free_variables = [cam.t, opt_pose[:3]]
ch.minimize(
# data term defined over torso joints...
{'cam': j2d[torso_cids] - cam[torso_smpl_ids],
# ...plus a regularizer for the camera translation
'cam_t': 1e2 * (cam.t[2] - init_t[2])},
x0=free_variables,
method='dogleg',
callback=on_step,
options={'maxiter': 100,
'e_3': .0001,
# disp set to 1 enables verbose output from the optimizer
'disp': 0})
In the beginning, the camera’s translation was initialized by similar triangle, the body orientation was initialized by mean pose.

After 11 iterations for this image, the optimization function converged.

Another return of this initialize_camera() function was the try_both_orient boolean variable. This was determined by the pixel distance between the predicted shoulder 2D joints.
1
2
# check how close the shoulder joints are
try_both_orient = np.linalg.norm(j2d[8] - j2d[9]) < pix_thsh
Step 4: Optimize body pose and shape
This is the core optimization of the pose estimate process, here will fit the model to the given set of 2D joints with the given estimated camera and body orientation. If the flag try_both_orient is true, the model will be fit twice for the body orientation and flipped body orientation, in the end, choose the one with the lower error as the final estimated pose.
The code for optimization is listed below:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# run the optimization in 4 stages, progressively decreasing the
# weights for the priors
for stage, (w, wbetas) in enumerate(opt_weights):
_LOGGER.info('stage %01d', stage)
objs = {}
objs['j2d'] = obj_j2d(1., 100)
objs['pose'] = pprior(w)
objs['pose_exp'] = obj_angle(0.317 * w)
objs['betas'] = wbetas * betas
if regs is not None:
objs['sph_coll'] = 1e3 * sp
ch.minimize(
objs,
x0=[sv.betas, sv.pose],
method='dogleg',
callback=on_step,
options={'maxiter': 100,
'e_3': .0001,
'disp': 0})
- Data Term - objs[‘j2d’]: distance between observed and estimated joints in 2D, like the previous step, the goal is to minimize the distance between predicted 2D joints and the projected SMPL joints.
1 2 3
# data term: distance between observed and estimated joints in 2D obj_j2d = lambda w, sigma: ( w * weights.reshape((-1, 1)) * GMOf((j2d[cids] - cam[smpl_ids]), sigma))The equation is shown in the image below,
![Eq]() \
\ - Prior Pose Term - objs[‘pose’]: Here the GMM created in step 2 was used
![Eq]() \
\ - Joint angles pose prior term for elbow and knee - objs[‘pose_exp’]: to penalty unnatural pose of elbow and knee
1 2 3 4 5 6 7 8 9
# joint angles pose prior, defined over a subset of pose parameters: # 55: left elbow, 90deg bend at -np.pi/2 # 58: right elbow, 90deg bend at np.pi/2 # 12: left knee, 90deg bend at np.pi/2 # 15: right knee, 90deg bend at np.pi/2 alpha = 10 my_exp = lambda x: alpha * ch.exp(x) obj_angle = lambda w: w * ch.concatenate([my_exp(sv.pose[55]), my_exp(-sv.pose[ 58]), my_exp(-sv.pose[12]), my_exp(-sv.pose[15])])![Eq]()
- Interpenetration error term - objs[‘sph_coll’]: to penalty interpenetration
1 2 3 4 5
if regs is not None: # interpenetration term sp = SphereCollisions( pose=sv.pose, betas=sv.betas, model=model, regs=regs) sp.no_hands = True![Eq]()
- Shape prior term - objs[‘betas’]: to penalty shape parameters derivated from the mean shape.
![Eq]()

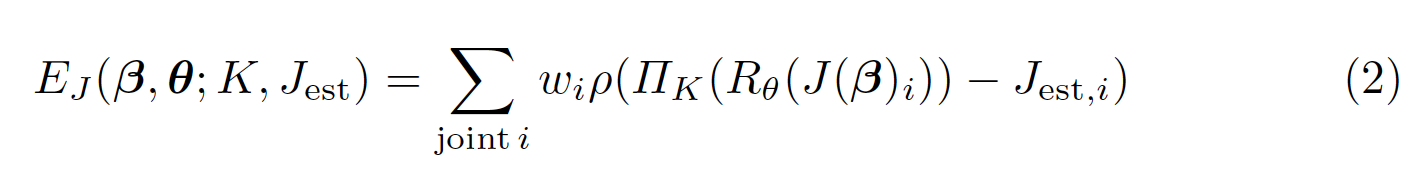 \
\